[최소신장트리] MTS(Minimum Spanning Tree) / Kruskal's Algorithm / Prim’s Algorithm

https://school.programmers.co.kr/learn/courses/30/lessons/42861

📌 MST (Minimum Spanning Tree, 최소 신장 트리)란?

➡ "모든 정점을 연결하는 간선들의 부분집합 중, 최소 비용으로 연결할 수 있는 트리"

➡ Greedy(탐욕법) 알고리즘을 기반으로 동작

---

1. MST(최소 신장 트리)의 특징

https://www.geeksforgeeks.org/spanning-tree/

Spanning Tree - GeeksforGeeks

 

• 신장 트리(Spanning Tree): 그래프의 모든 정점을 포함하면서 사이클이 없는 트리 형태

사이클이란?

📌 "사이클이 없다"는 의미

사이클(Cycle)이 없다는 것은 그래프 내에서 시작한 정점으로 돌아올 수 없는 구조를 의미합니다.

 

📌 사이클이 없다는 것이 "단방향"을 의미하는가?

➡ "사이클이 없다는 것"은 "단방향"과는 다른 개념입니다!
➡ 그래프가 유향(방향이 있음)인지 무향(방향이 없음)인지와는 별개로 사이클이 있을 수도, 없을 수도 있음.

 

✅ 사이클 없음(Acyclic) → "어떤 정점에서 출발해도 다시 돌아올 수 없는 구조"
✅ 단방향(Directed) → "방향성이 있는 그래프 (유향 그래프)"

✅ 즉, 방향 그래프(Directed Graph)에서도 사이클이 있을 수도 있고, 없을 수도 있음!

 

 

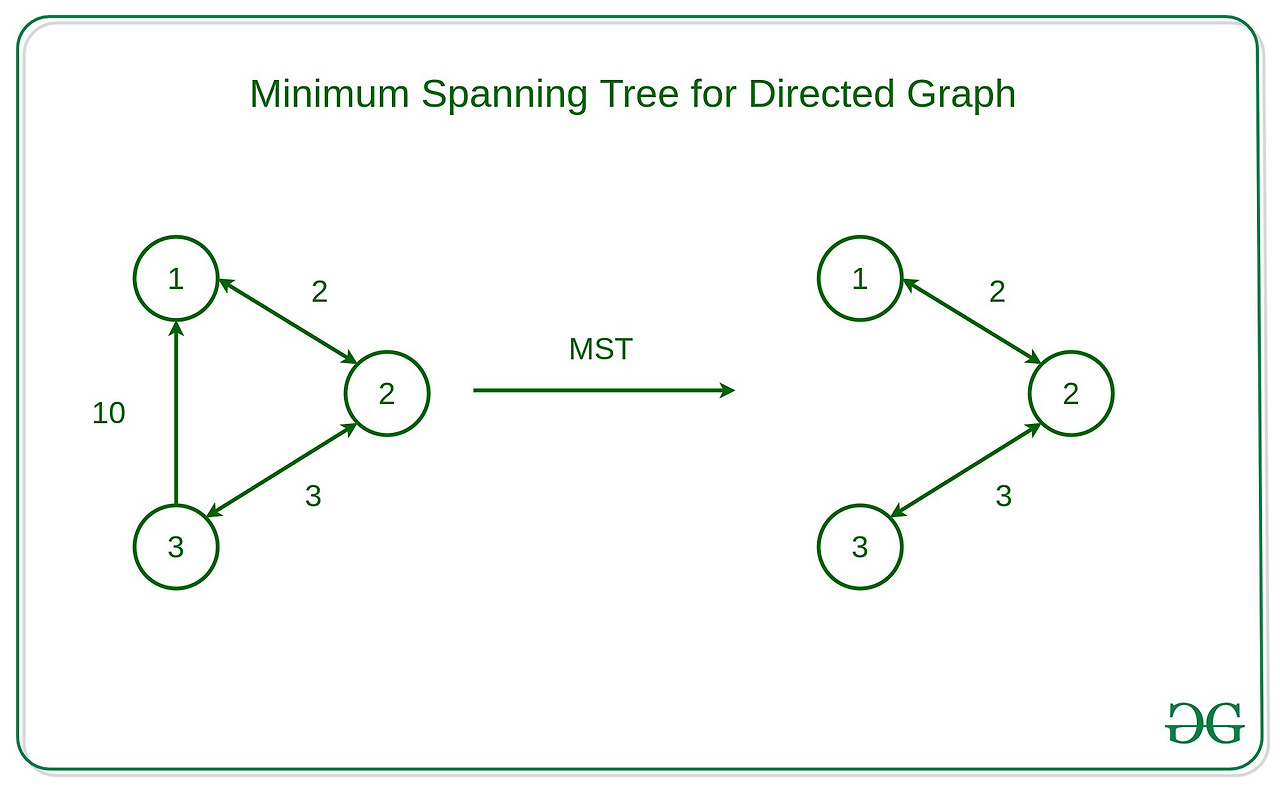
• 최소 신장 트리(MST, Minimum Spanning Tree): 모든 정점을 연결하는 신장 트리 중 간선의 가중치 합이 최소가 되는 트리
• N개의 정점이 있다면 MST의 간선 개수는 N-1개  --> 위 그림을 참고하면, 3개의 정점(노드)와 2개의 간선으로 이루어짐을 알 수 있다.

 

• 대표적인 알고리즘: 크루스칼(Kruskal), 프림(Prim)

---

✅ 크루스칼 알고리즘 (Kruskal's Algorithm) - 간선 중심 (Edge-based) 알고리즘

• 간선을 가중치 기준으로 정렬
• 가장 작은 가중치의 간선부터 선택
• 사이클이 생기지 않으면 Union-Find로 합치기
• N-1개의 간선을 선택하면 종료 (MST 완성)
• ✅ 모든 정점을 연결하면서, 가중치 합이 최소가 되도록 함
• 시간 복잡도: O(E log E) (간선 정렬 + 유니온 파인드)
• 📌 유니온 파인드 (Union-Find)란? ---- 업데이트 필요

➡ "서로소 집합(Disjoint Set)"을 효율적으로 관리하는 알고리즘
➡ "두 개의 원소가 같은 집합에 속하는지 확인하고, 서로 다른 두 집합을 합치는 연산"을 빠르게 수행하는 자료구조

✅ 대표적인 활용 예시:

1. MST(최소 신장 트리) - 크루스칼 알고리즘 (사이클 검출)
2. 그래프에서 사이클 판별
3. 네트워크 연결 여부 확인
4. 도시 분할, 같은 집단인지 판별하는 문제

📌 유니온 파인드의 핵심 연산

연산설명시간 복잡도 (경로 압축 적용)

Find(x)	x가 속한 집합(루트 노드) 찾기	O(α(N)) (거의 O(1))
Union(x, y)	x와 y의 집합을 합치기	O(α(N)) (거의 O(1))

📌 유니온 파인드의 핵심은 "경로 압축 (Path Compression)"을 통해 시간 복잡도를 줄이는 것!

# 크루스칼 알고리즘 (Union-Find 활용)
import sys

def find(parent, x):
    if parent[x] != x:
        parent[x] = find(parent, parent[x])
    return parent[x]

def union(parent, a, b):
    rootA = find(parent, a)
    rootB = find(parent, b)
    if rootA != rootB:
        parent[rootB] = rootA

def kruskal(n, edges):
    edges.sort(key=lambda x: x[2])  # 가중치 기준 정렬
    parent = {i: i for i in range(n)}
    mst_cost = 0
    mst_edges = []

    for u, v, weight in edges:
        if find(parent, u) != find(parent, v):
            union(parent, u, v)
            mst_edges.append((u, v))
            mst_cost += weight

    return mst_cost, mst_edges

# 예제 입력
edges = [
    (0, 1, 1), (0, 2, 3), (1, 3, 4), (3, 5, 2), (2, 4, 3), (4, 5, 2)
]
n = 6  # 정점 개수

print(kruskal(n, edges))  # (최소 비용, MST 간선 리스트)

 

관련 코딩 테스트 문제 [섬 연결하기]

https://school.programmers.co.kr/learn/courses/30/lessons/42861

프로그래머스

 

---

✅ 프림 알고리즘 (Prim’s Algorithm)

• 한 정점에서 시작하여 가장 작은 가중치의 간선을 선택해 확장
• 우선순위 큐(Priority Queue, Min-Heap) 사용
• 시간 복잡도: O(E log V) (우선순위 큐 사용)

# 프림 알고리즘 (Min-Heap 활용)
import heapq

def prim(n, adj):
    mst_cost = 0
    visited = [False] * n
    pq = [(0, 0)]  # (가중치, 시작 정점)
    mst_edges = []

    while pq:
        weight, u = heapq.heappop(pq)
        if visited[u]: continue  # 이미 방문한 정점이면 건너뜀
        visited[u] = True
        mst_cost += weight

        for v, w in adj[u]:
            if not visited[v]:
                heapq.heappush(pq, (w, v))
                mst_edges.append((u, v))

    return mst_cost, mst_edges

# 예제 입력
n = 6  # 정점 개수
adj = {  # 인접 리스트
    0: [(1, 1), (2, 3)], 1: [(3, 4)], 2: [(4, 3)], 3: [(5, 2)], 4: [(5, 2)]
}

print(prim(n, adj))  # (최소 비용, MST 간선 리스트)

 

 

📌 크루스칼 알고리즘(Kruskal's Algorithm) vs 프림 알고리즘(Prim’s Algorithm)

➡ "MST(최소 신장 트리, Minimum Spanning Tree)를 찾는 알고리즘"
➡ 각 알고리즘이 어떤 문제 해결에 적합한지 비교

---

1. Kruskal’s Algorithm (크루스칼 알고리즘)

✅ 특징:

• "간선 중심(Greedy)" 방식
• 모든 간선을 가중치 기준으로 정렬한 후, 작은 것부터 하나씩 선택
• **유니온-파인드(Union-Find)**를 사용하여 사이클을 방지
• 그래프가 "간선 중심(Edge-based)"일 때 유리

✅ 적합한 문제 유형:

• 간선이 적은 그래프(Sparse Graph, E ≈ V)
• 개별적인 연결된 그룹이 존재하는 경우(Disconnected Graph 포함)
• 사이클이 존재하는지 판별해야 하는 경우
• 입력으로 간선 리스트만 주어지는 경우

✅ 시간 복잡도:

• O(E log E) (간선 정렬 + 유니온-파인드 O(α(N)))

✅ 실제 활용 예시:

• 네트워크 연결 최적화 (LAN 케이블 설치, 전력망 최적화)
• 도로 건설 비용 최적화
• 컴퓨터 네트워크 간선 연결 비용 최소화
• 그래프에서 사이클을 찾아야 하는 경우

✅ 대표적인 문제:

• 백준 1197번 - 최소 스패닝 트리
• 백준 4386번 - 별자리 만들기

---

 

2. Prim’s Algorithm (프림 알고리즘)

✅ 특징:

• "정점 중심(Greedy)" 방식
• 한 정점에서 시작하여, 방문한 정점에서 연결할 수 있는 가장 가중치가 작은 간선을 선택
• 우선순위 큐(힙, Priority Queue, Min-Heap) 사용하면 효율적
• 그래프가 "정점 중심(Vertex-based)"일 때 유리

✅ 적합한 문제 유형:

• 간선이 많은 그래프(Dense Graph, E ≈ V²)
• 완전 연결 그래프(Fully Connected Graph)
• 모든 정점이 연결된 하나의 네트워크를 만들고 싶을 때
• 인접 리스트가 주어지고, 특정 정점에서 시작해야 하는 경우

✅ 시간 복잡도:

• O(E log V) (우선순위 큐 사용 시)

✅ 실제 활용 예시:

• 항공 네트워크 구축 (가장 효율적인 루트 연결)
• 도시 도로 네트워크 최적화
• 게임에서 맵 생성 (최소한의 벽을 사용하여 길 연결)

✅ 대표적인 문제:

• 백준 1922번 - 네트워크 연결
• 백준 6497번 - 전력난

 

---

3. Kruskal vs Prim 비교 (어떤 문제에 적합?)

	크루스칼(Kruskal)	프림(Prim)
알고리즘 유형	간선 중심 (Edge-based)	정점 중심 (Vertex-based)
핵심 자료구조	유니온-파인드 (Union-Find)	우선순위 큐 (Min-Heap)
그래프 유형	희소 그래프(Sparse Graph, E ≈ V)	밀집 그래프(Dense Graph, E ≈ V²)
사이클 검출	✅ 가능 (유니온-파인드 활용)	❌ 불가능
초기 실행 방식	간선 정렬 후 작은 간선부터 추가	임의의 정점에서 시작하여 확장
분리된 그래프 처리	✅ 가능 (Disconnected Graph도 다룰 수 있음)	❌ 불가능 (하나의 연결된 그래프에서만 동작)
시간 복잡도	O(E log E)	O(E log V)
적합한 문제 유형	간선 리스트만 주어진 경우, 분리된 그래프 포함	완전 연결 그래프, 특정 정점에서 시작하는 경우

---

4. 결론: 어떤 알고리즘을 써야 할까?

• "간선 개수가 적고, 간선 리스트가 주어진 경우" → Kruskal (O(E log E))
• "간선 개수가 많고, 정점 중심으로 확장해야 하는 경우" → Prim (O(E log V))
• "사이클을 판별해야 하는 경우" → Kruskal (유니온-파인드 활용)
• "분리된 그래프(Disconnected Graph)에서도 적용해야 하는 경우" → Kruskal

📌 즉, 문제 유형에 따라 Kruskal과 Prim을 선택해야 함! 🚀